등급: 골드
문제
민식이는 수학학원에서 단어 수학 문제를 푸는 숙제를 받았다.
단어 수학 문제는 N개의 단어로 이루어져 있으며, 각 단어는 알파벳 대문자로만 이루어져 있다. 이때, 각 알파벳 대문자를 0부터 9까지의 숫자 중 하나로 바꿔서 N개의 수를 합하는 문제이다. 같은 알파벳은 같은 숫자로 바꿔야 하며, 두 개 이상의 알파벳이 같은 숫자로 바뀌어지면 안 된다.
예를 들어, GCF + ACDEB를 계산한다고 할 때, A = 9, B = 4, C = 8, D = 6, E = 5, F = 3, G = 7로 결정한다면, 두 수의 합은 99437이 되어서 최대가 될 것이다.
N개의 단어가 주어졌을 때, 그 수의 합을 최대로 만드는 프로그램을 작성하시오.
입력
첫째 줄에 단어의 개수 N(1 ≤ N ≤ 10)이 주어진다. 둘째 줄부터 N개의 줄에 단어가 한 줄에 하나씩 주어진다. 단어는 알파벳 대문자로만 이루어져있다. 모든 단어에 포함되어 있는 알파벳은 최대 10개이고, 수의 최대 길이는 8이다. 서로 다른 문자는 서로 다른 숫자를 나타낸다.
출력
첫째 줄에 주어진 단어의 합의 최댓값을 출력한다.
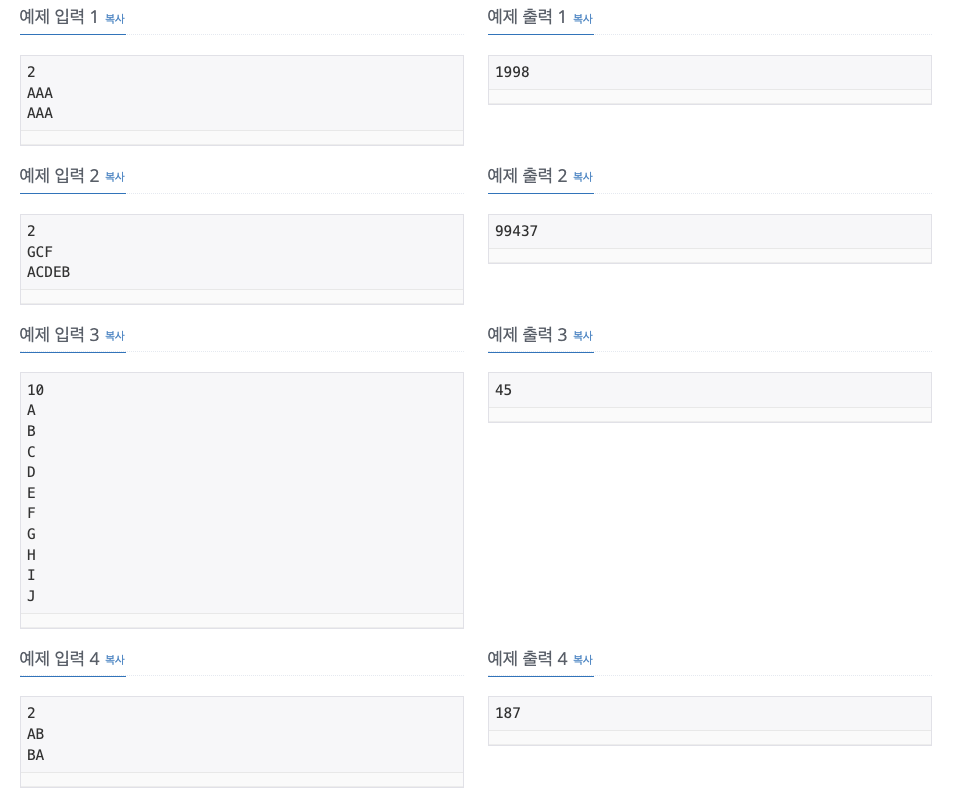
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
n = int(input())
words = []
alphabets = {}
for _ in range(n):
words.append(input())
for w in words:
square_root = len(w)-1
for l in w:
if l in alphabets:
alphabets[l] += pow(10,square_root)
else:
alphabets[l] = pow(10,square_root)
square_root-=1
alphabets_s = sorted(alphabets.values(),reverse=True)
sum = 0
num = 9
for i in alphabets_s: #0-9
sum += i * num
num-=1
print(sum)
문제 주요 Key:
- 자릿수가 높은 순서로 높은 값 (0-9)을 부여해야 최댓값이 나옴
- 약간의 계산을 실험 삼아서 해보면 금방 알 수 있다.
- 자료형은 배열과 딕셔너리를 사용한다.
- 배열은 단어들을 담는다. ([’AAA’, ‘BBB’])
- 딕셔너리는 영문자를 key로, 자릿수값을 value로 갖는다.
- ex. A는 1000의 자리라면 {A:1000}
- A가 100의 자리에서 한번 더 나오게 되면 {A:1100}이 됨
- ex. A는 1000의 자리라면 {A:1000}
- 100의 자리라면 10의 2제곱, 10의 자리라면 10의 1제곱 (pow()를 사용한다.)
- 이중 for문으로 접근한다.
- 첫번째 for문은 words 배열에 접근해서 해당 word의 길이를 10에 제곱할 값으로 삼는다. (마지막은 1의 자리라서 len(w)에 1을 빼준다)
- 두번째 for문은 해당 word의 각 letter (영문자)에 접근해서 해당 글자가 이미 dict에 존재한다면 10의 자릿수를 제곱한 값을 더하고, 아니라면 추가한다.
- 최댓값을 구하는 것이기 때문에 9에서 -1을 해가면서, 자릿수가 많은 값부터 곱해서 결과값에 더 할 것이다.
- 9에서 -1을 해가면서 곱할 것이기 때문에 딕셔너리 (alphabets)를 내림차순으로 정렬한다.
느낀 점:
- 알고리즘 문제를 풀면서 주로 딕셔너리를 안 사용하고도 풀렸어서, 이를 사용하지 않는 더 쉬운 방식이 있을거라고 생각하고 접근함 → 결과적으로 더 어려워짐
- 생각했다면 아마 영문자와 자릿수를 mapping하는 방식으로 딕셔너리를 구성하게 될 거라는거를 떠올릴 수 있었을 것
- 파이썬에서 pow()를 사용 안해봐서 이 또한 떠올리지 못함
- 구현력 부족
- 못 풀더라도 이러한 문제를 많이 접해보고 접근 방식을 역추적해서 배워야겠다고 느낌
- 구현력 부족
- 영문자가 다른 자릿수에서 중복되어서 나타난다면, dict값에서 더해주면 될텐데, 따로 처리해주어야 된다고 생각함
- 수학적 사고의 부족
- 더 단순하게 할 수 있는거를 문자에서 표기된 방식 그대로, 혹은 일차원적으로 접근하는 경향이 있음
- 수학적 사고의 부족
